Metode biseksi ini adalah metode untuk mencari akar-akar dari sebuah fungsi dengan cara menghitung nilai fungsi f(x) dari 2 nilai X : (X1,X2) yang diberikan, dan diharapkan nilai f(X1).f(X2)< xmid="(X1+X2)/2." baru =" (Xmid">
Metode numerik untuk mendapatkan harga x untuk f(x) = 0 seperti uraian di pasal 2.1 disebut METODE BISECTION. Tahap pertama proses adalah menetapkan nilai sembarang a dan b sebagai batas segmen nilai fungsi yang dicari. Batasan a dan b memberikan harga bagi fungsi f(x) untuk x = a dan x = b. Langkah selanjutnya adalah memeriksa apakah f(a)×f(b) <>
Dengan rumusan m = (a+b)/2, diperiksa apakah nilai mutlak f(m) <>-6 (batas simpangan kesalahan). Jika benar, nilai x = m adalah solusi yang dicari. Jika tidak terpenuhi, ditetapkan batasan baru dengan mengganti nilai b = m apabila f(a)*f(m) < a =" m"> 0; proses menemukan m baru dilakukan seperti prosedur yang telah dijelaskan.
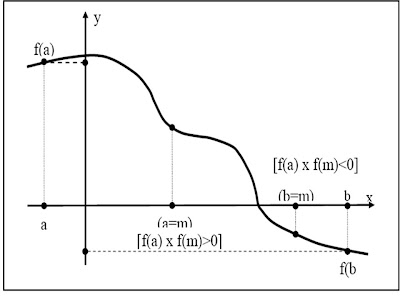
Metode Bisection adalah salah satu kelas metode Pengelompokan, karena prosedur untuk mendapatkan nilai x untuk f(x) = 0 dilakukan melalui pendekatan kelompok akar. Metode ini tidak sepenuhnya memanfaatkan data f(x) bagi penentuan nilai x. Misalnya, tidak digunakannya ukuran relatif f(a) dan f(b), karena umumnya jika f(a) <>
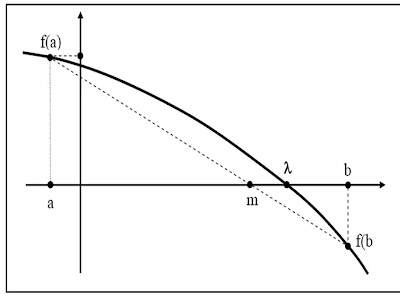
Metode Bisection ini paling sederhana dan paling intractif dari metode pendekatan berturut-turut untuk melokalisasi sebuah persamaan akar f(x) = 0 dalam selang [a,b].
Metode ini didasrkan pada teorema nilai antara untuk fungsi kontinu., yang menyatakan pada suatu selang [a,b] sedemikian sehingga titik-titik ujung f berlawanan tanda, missal f(a) <> 0, harus mengandung suatu akar. Metode ini merupakan pengulangan pembagiduaan selang yang memenuhi teorema di atas. Oleh karena itu metode ini disebut metode bagi dua.
Algoritma Metode Bisection
Asumsi awal yang harus diambil adalah: ‘menebak’ interval awal
[a,b] dimana f(x) adalah kontinu padanya, demikian pula harus
terletak ‘mengapit’ (secara intuitif) nilai akar a, sedemikian rupa
sehingga:
f (a) × f (b) £ 0
Algoritma BISECT(f,a,b,akar,e,iter,itmax,flag)
1. Tebak harga interval [a,b]; tentukan e; dan itmax
2. Set f0 = f(a); iter = 0; flag = 0;
3. Tentukan atau hitung akar = c := (a + b)/2; iter = iter + 1;
4. Jika f(a)·f(c) £ 0 maka b = c jika tidak a = c dan f0 = f(a);
5. Jika (b – a) £ e maka flag = 1 jika iter >itmax maka flag = 2;
6. Jika flag = 0 ulangi ke nomor 3;
7. Akar persamaan adalah: akar = (a + b)/2,sebagai akar terbaru;
8. Selesai.
Listing Program Metode Bisection
Diberikan persoalan untuk mengitung akar (akar-akar) persamaan f(x) = 0, sebagai berikut: f (x) º x - e1 x = 0
Listing program sederhana (non-subroutine) dan program dengan subroutine disertakan dalam gambar-gambar 5.2. dan 5.3. di bawah ini, yang ditulis dalam Bahasa FORTRAN 77 (kompatibel dengan Bahasa FORTRAN 90/95).
Bagan Alir Metode Bisection:
1. Pemrograman C Untuk Metode Bisection
Metode Numerik
LISTING PROGRAM BISECTION METHODE
( BAHASA PEMROGRAMAN TURBO C)
#include
#include
#include
#include
double fx(double x)
{
double coef[]={25.0,0.6};
return poly(x,3,coef);
}
double bisect(double a,double b,double eps)
{
double xl=a,xr=b,epsb,xm,fxl,fxm,abseps;
xm=0.5*(xl+xr);
printf("--------------------------------------------------------------------------------");
printf(" xl xr xm |xm-xl| f(xl) f(xm) f(xl)*f(xm)\n");
printf("--------------------------------------------------------------------------------");
do
{
abseps=fabs(xm-xl);
fxl=fx(xl);
fxm=fx(xm);
epsb=fxl*fxm;
printf("%10.5f%10.5f%10.5f%10.5f%10.5f%10.5f10.5f\n",xl,xr,xm,abseps,fxl,fxm,epsb);
if(epsb<0.0)
xr=xm;
else
xl=xm;
xm=0.5*(xl+xr);
}while(abseps>=eps);
return xm;
}
main()
{
double a=34,b=35,eps=1.0e-5,x,c;
clrscr();
printf(" Penjadwalan Unit Pembangkit dengan Metode Bisection\n ");
printf("\n");
printf("\n");
printf("Nama : Dwiyanto\n");
printf("NIM : 021910201023\n");
printf("Jurusan : Teknik Elektro S1\n");
printf("\n");
printf("Berapa jumlah total beban (MW) ?");
scanf("%f",&c);
printf(“Jika anda ingin mengubah jumlah total beban, silahkan anda ganti nilai awal”);
printf("nilai awal %f dan %f\n",a,b);
printf("Ketelitian %f\n",eps);
x=bisect (a,b,eps);
printf(“Tekan ENTER untuk stop”);
getch();
}
2. Pemrograman Metode Bisection Menggunakan QBasic
CLS
SCREEN 0
COLOR 3,0,0
CLS
LOCATE 2,8:PRINT CHR$(201); STRING$(58,205); CHR$(187)
FOR I = 3 TO 22
LOCATE i, 8: PRINT CHR$(186); STRING$(58,” ”);CHR$(186)
NEXT i
LOCATE 23,8:PRINT CHR$(200); STRING$(58,205); CHR$(188)
COLOR 3,0,0
LOCATE 3,12:PRINT “=================================================”
LOCATE 4,12:PRINT ” PROGRAM MENCARI AKAR PERSAMAAN “
LOCATE 5,12:PRINT “ Oleh : Ferdian Rahabista “
LOCATE 6,12:PRINT “ Metode : BISECTION “
LOCATE 7,12:PRINT “=================================================”
DEF fnz(x) = 3*x^3+4*x-7
LOCATE 9,10: PRINT “Bentuk Fungsinya :f(x)=3*x^3+4*x-7”
LOCATE 10,10: PRINT “Buat Pendugaan akar ini pada selang [a,b]”
btanda = 10
WHILE(btanda <> 1)
LOCATE 12,10: PRINT “input nilai a = “
LOCATE 13,10: PRINT “input nilai b = “
LOCATE 14,10: PRINT “input nilai toleransi = “
LOCATE 12,10: PRINT “isikan nilai a =”,a
LOCATE 13,10: PRINT “isikan nilai b =”,b
IF a>b THEN
LOCATE 15,15: PRINT “Nilai a harus kurang dari b”
INPUT “”,BOM
GOTO SATU:
END IF
LOCATE 14,10: INPUT “inputan nilai toleransi =”,tol
IF tol = 0 THEN
LOCATE 15,15: PRINT “Nilai tol harus diisi”
INPUT “”,BOM
GOTO SATU:
END IF
h = 01
n = ABS((b-a)/h)
btanda = 0
tanda1 = SGN(fnz(a))
FOR i=1 TO n+1
tanda2=SGN(fnz(h*(i-1)+a))
‘PRINT h*(-1) + a,tanda2
If tanda1 <> tanda2 THEN
IF tanda1 <> 0 THEN
Btanda=btanda+1
END IF
tanda1=tanda2
END IF
NEXT i
IF btanda = 0 THEN
LOCATE 16,10: PRINT “pada selang [“; a; “,”;b;”] tidak terdapat”
COLOR 18,8,0: LOCATE 18,18: PRINT “mohon inputkan a&b diulang”
COLOR 3,0,0
ELSE
IF btanda > 1 THEN
‘LOCATE 16,10: PRINT “pada selang [“;a;”,;b;” : PRINT USING “]”;
‘COLOR 18,8,0: LOCATE 18,18: PRINT “mohon inputkan a&b diulang”
‘COLOR 3,0,0
‘ LOCATE 20,20: INPUT “ulangi dengan menekan <
‘LOCATE 20,20: PRINT “”
END IF
ELSE
LOCATE 16,10: PRINT “tepat, pada selang [“;a;”,”;b;”: PRINT USING “]”;
LOCATE 17,10: PRINT “”
COLOR 18,8,0:LOCATE 18,18: PRINT “anda benar memasukkan selang nilai”
COLOR 3,0,0
LOCATE 20,20: PRINT “isikan nilai toleransi unutk f(x)”
END IF
WEND
COLOR 3,0,0
LOCATE 12,10: PRINT USING “nilai a=###.###”;a
LOCATE 13,10: PRINT USING “nilai b=###.###”;b
LOCATE 14,10: PRINT USING “toleransi=###.###”;tol
LOCATE 18,18: PRINT “”
LOCATE 20,20: PRINT “”
CLS
PRINT “mencari akar dengan metode BISECTION”
PRINT “bentuk fungsinya : f(x)=3*x^3+4*x-7”
PRINT”nilai toleransi tol =”;tol
C$=”###:##.##### :##.##### :##.##### :##.##### :##.##### :##.##### :”
PRINT “=================================================”
PRINT “iter: a : b : f(a) : f(b) : c : f(c) :”
PRINT”---------------------------------------------------------------------------------------“
Iter=0
Y=tol
WHILE(ABS(y)>=tol)
C=(a+b)/2
‘c=a-fnz(a)*(b-a)/(fnz(b)-fnz(a))
Y=fnz(c)
PRINT USING c$; iter, a, b, fnz(a), fnz(b), c, fnz(c)
Iter = iter+1
IF(fnz(a)*fnz(c)>0) THEN
A = c
ELSE
b=c
END IF
WEND
PRINT “=================================================”
PRINT USING “nilai akar = ##.##### pada x = ##.#####”; fnz(c),c
PRINT USING”jumlah iterasi =#### kali”;iter
COLOR 3,0,0: PRINT “jika anda telah puas, tekan <
LG$ = “Y”
INPUT “COBA LAGI (Y/T);”,LG$
IF LG$ = “Y” OR LG$ = “y” THEN
GOTO SATU:
ELSE
END IF


















4 Responses So Far:
thanks
kebetulan q lagi cari tentang dasar teori metode biseksi
ANGKA2 TAK DA GUNA DIKEHIDUPAN!!!!
DASAR ADMIN MUKE GILE!!
sastro_pedal@rocketmail.com
Saya setuju sama pendpt si Anonim:"ANGKA2 TAK DA GUNA DIKEHIDUPAN!!!!"
Buat apa coba, jual beli gak serumit itu, program kompt gak sy jumpai kyak gt, faktur juga enggak....!!!! TRus Matematika yg RUMIT-RUMIT buat apa,, dimasukkin UN atau UAS pasti rata2 pd mengurangi Nilai rata2 Kita... fuck mtk